La potenciación es
una operación matemática entre dos términos denominados: base a y
exponente n. Se escribe an y
se lee usualmente como «a elevado a n»
o «a elevado a la» y el sufijo en
femenino correspondiente al exponente n.
Su definición varía según el conjunto numérico al que pertenezca el exponente:
- Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.

Por ejemplo:  .
.
- Cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.

- Cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
![a^{\frac{n}{m}} = \sqrt[m]{a^n}](http://upload.wikimedia.org/wikipedia/es/math/3/9/8/3983643a5db08e21da69fffabbc0875c.png)
Cualquier número elevado al exponente  el resultado equivale a
el resultado equivale a  , excepto el caso particular de
, excepto el caso particular de  que, en principio, no está definido (ver cero).
que, en principio, no está definido (ver cero).
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Propiedades de los exponentes

 .
.
![a^{\frac{n}{m}} = \sqrt[m]{a^n}](http://upload.wikimedia.org/wikipedia/es/math/3/9/8/3983643a5db08e21da69fffabbc0875c.png)
 el resultado equivale a
el resultado equivale a  , excepto el caso particular de
, excepto el caso particular de  que, en principio, no está definido (ver cero).
que, en principio, no está definido (ver cero).-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Propiedades de los exponentes
Potencia de exponente 0
Un número distinto de 0 elevado al exponente 0 da como resultado la unidad (1), puesto que:
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base:
Ejemplo:
Potencia de exponente negativo
Un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero con exponente positivo:
Multiplicación de potencias de igual base
El producto de dos potencias que tienen la misma base es igual a una potencia de dicha base que tiene como exponente la suma de los exponentes, es decir:
Ejemplos:
División de potencias de igual base
El cociente de dos potencias que tienen la misma base es igual a una potencia de dicha base que tiene como exponente el resultado de restar el exponente del divisor al del dividendo, es decir:
Ejemplo:
Potencia de un producto
La potencia de un producto es igual al producto de cada uno de los factores elevado al mismo exponente, es decir:
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):
Debido a esto, la notación  se reserva para significar
se reserva para significar  ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como  .
.
 se reserva para significar
se reserva para significar  ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como  .
.Potencia de un cociente
La potencia de un cociente es igual al cociente de cada uno de los números elevado al mismo exponente.
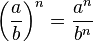 -------------------------------------------------------------------------------------------------------------------------------------------------------------Radicación
-------------------------------------------------------------------------------------------------------------------------------------------------------------Radicación
En matemática, la radicación de orden n de un número a es cualquier número b tal que , donde n se llama índice u orden, a se denomina radicando, y b es una raíz enésima, por lo que se suele conocer también con ese nombre. La notación a seguir tiene varias formas:
, donde n se llama índice u orden, a se denomina radicando, y b es una raíz enésima, por lo que se suele conocer también con ese nombre. La notación a seguir tiene varias formas:![y = \sqrt[n]{x} = x^{1/n}](http://upload.wikimedia.org/wikipedia/es/math/d/a/0/da08201213a1c583a35ad8551b7033a1.png) .
.
Para todo n natural, a y b reales positivos, se tiene la equivalencia:![a = b^n \iff b = \sqrt[n]{a}](http://upload.wikimedia.org/wikipedia/es/math/c/9/9/c99b9f1ded801acbedaec4892e4a9cfd.png) .
.- __________________________________________________________________________________
- Como se indica con la igualdad
![y = \sqrt[n]{x^m} = x^{m/n},](http://upload.wikimedia.org/wikipedia/es/math/1/1/c/11c840d337b1a08da4f57c1b643bc686.png) la radicación es en realidad otra forma de expresar una potenciación: la raíz de un cierto orden de un número es equivalente a elevar dicho número a la potencia inversa. Por esto, las propiedades de la potenciación se cumplen también con la radicación.
la radicación es en realidad otra forma de expresar una potenciación: la raíz de un cierto orden de un número es equivalente a elevar dicho número a la potencia inversa. Por esto, las propiedades de la potenciación se cumplen también con la radicación.- Ejemplo
![\sqrt[4]{x^3}](http://upload.wikimedia.org/wikipedia/es/math/b/a/e/baebf0599dd68b8b187849ab5bfe85f5.png) =
= 
Raíz de un productoLa raíz de un producto es igual al producto de las raíces de los factores.con n distinto de cero (0).- Ejemplo
 =
=  =
= 
Se llega a igual resultado de la siguiente manera:
Raíz de un cocienteLa raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador.![\sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}}](http://upload.wikimedia.org/wikipedia/es/math/a/e/a/aeaab0bb87839a08a18f6665da55b7c8.png) =
= ![\frac{\sqrt[n]{a}}{\sqrt[n]{b}}](http://upload.wikimedia.org/wikipedia/es/math/2/3/a/23a8eeedd627fa6e0d34459126509315.png)
con n distinto de cero (0).- Ejemplo
 =
= 
Cuando esta propiedad se aplica a números, no hace falta pasar la raíz a potencia de exponente racional, aunque sí cuando se hace con variables.- Ejemplos
![\sqrt[3]{\frac{x^3}{y^9}} = \frac{x^{3/3}}{y^{9/3}}](http://upload.wikimedia.org/wikipedia/es/math/6/5/9/6595a65cbeb38b385ee03383aecfe8d7.png) =
= 
![(\sqrt[4]{a^2})^8 = (\ a^{2/4})^8](http://upload.wikimedia.org/wikipedia/es/math/f/9/4/f94559ccddd6b689edeb0afe65e4f2d8.png) =
= ![\sqrt[4]{a^{16}}.](http://upload.wikimedia.org/wikipedia/es/math/9/f/6/9f6705379165137a12885d717eba2d9f.png)
Raíz de una raízPara calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando.![\sqrt[n]{\sqrt[m]{a}}](http://upload.wikimedia.org/wikipedia/es/math/e/1/e/e1e486e1baffef5cc022cf72ba8d800c.png) =
= ![\sqrt[n \cdot m]{a}.](http://upload.wikimedia.org/wikipedia/es/math/b/7/1/b712b3f923b961e0efe0a5339ae17110.png)
con n y m distintos de cero (0).- Ejemplo
![\sqrt[9]{\sqrt[3]{5}}](http://upload.wikimedia.org/wikipedia/es/math/e/c/c/ecccb85a5a8ea3da5c9db742f2f8cd8a.png) =
= ![\sqrt[27]{5}.](http://upload.wikimedia.org/wikipedia/es/math/6/0/4/60421728786d19fa3114266ce32140e2.png)

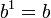
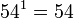







![\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}](http://upload.wikimedia.org/wikipedia/es/math/6/2/f/62ff232d8ae597f13efb5db26edc04cb.png)

No hay comentarios:
Publicar un comentario